Students’ conceptual understanding of multiplication involves much more than just repeated addition.
It is quite common to teach multiplication through repeated addition such as 2+2+2+2+2=10 to learn 2×5=10. However, this way of teaching is only part of what multiplicative thinking involves. For students to develop a deeper understanding of multiplication, teachers should consider engaging students in multiplicative double counting.
Think about a student building this problem using manipulatives: You have seven towers with three cubes in each; how many cubes do you have altogether?
In solving this problem there are three types of units: the towers (groups), the cubes per tower (unit rate), and the total amount of cubes altogether (the total resulting singles or 1s). A student who uses repeated addition would likely solve this problem by adding 3s—first by using the equation 3+3+3+3+3+3+3=? and then perhaps combining the 3s into groups (e.g., 3+3 is 6; 6+6 is 12; then 6 more is 18 and 3 more is 21).
But what units has the student tracked in doing this? Although arriving at the correct answer, most students using this strategy have tracked only two of the three units involved in multiplication. They have successfully tracked the cubes per tower (3 each) and the accrual of cubes (singletons), but not the number of groups (towers) counted in this process.
Student using manipulatives to show thinking on how to solve 7×3 using repeated addition as a strategy to solve.
Multiplicative double counting, unlike repeated addition, involves students’ ability to keep track of all three units as they work to solve a multiplication problem. A student using multiplicative double counting would solve the above problem by tracking the amount of towers they had counted, either with their fingers, a drawing, or another form. They would also track the unit rate and total amount of singletons. For example, they may simultaneously hold up one finger and say “three cubes,” then hold another finger and say “six cubes,” and continue all the way to seven fingers and 21 cubes. In this situation, the student is using their fingers to track the number of towers (groups) counted while also tracking three cubes per tower and the total amount of cubes.
The key to multiplicative double counting is that a student can be stopped in their counting sequence at any point and asked: How many towers have you counted? When asked, the student could tell you how many groups could be counted, as well as how many cubes per group and how many total cubes counted so far. This ability is not necessarily available to students who are simply using repeated addition, as they are likely not paying attention to the amount of groups they have counted as they are counting them.
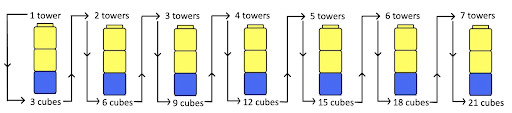
Reasoning involved in multiplicative double counting using 7 towers with 3 cubes each for a total of 21 cubes or 7×3=21.
By teaching students to solve multiplication situations using multiplicative double counting instead of repeated addition, students’ conceptual grounding for multiplication is further established. Their ability to track three units instead of two helps their readiness for future mathematics concepts including division, fraction, ratio and proportion, and algebra.
To advance students’ thinking beyond repeated addition and towards multiplicative double counting, consider the playful activity of Please Go Bring for Me (PGBM). PGBM begins with concrete materials (cubes), then moves students towards figural representations of the concrete materials, and ultimately ends with moving students toward an abstract way of thinking using symbols and equations.
For more information on how to implement PGBM in your classroom and move your students toward a more conceptual understanding of multiplication, see the recently published article, “Beyond Getting Answers: Promoting Conceptual Understanding of Multiplication.” And to learn more about our current research conversations, subscribe to Digital Promise’s Learning Sciences Connections newsletter to read stories that share useful findings from the field.
