School districts across the U.S. are reporting that English learners have been disproportionately affected academically by the lingering effects of the COVID-19 pandemic, in some cases scoring lower than researchers anticipated on math and English language arts assessments. School leaders are examining effective interventions, from high-dosage tutoring and summer learning programs to reductions in class sizes. However, improvement should start by addressing the core of mathematics instruction, not only by intervening when core instruction does not sufficiently support English learners (EL).
In a recent webinar hosted by Digital Promise titled “Mathematics and Language: Supporting English Learners in Mathematics Classrooms,” Dr. Judit Moschkovich, professor of mathematics education at University of California, Santa Cruz, shared her research on core instructional practices for teaching mathematics to English learners. The attendees, who represented school districts, universities, non-profits, and curriculum developers, engaged in roundtable discussions where they shared reflections and implications for their contexts. The presentation is available to view now.
Dr. Moschkovich explained that more than 30 years of research have shown that effective mathematics instruction begins with high expectations. Dr. Moschkovich described high expectations as teaching that presents all students with challenging mathematics and gives students time and support to engage in productive struggle. An important dimension of challenging mathematics is that it is not just about choosing the right procedure to quickly find a single right answer; rather, in advanced mathematics courses and in professions using mathematics, problem solving with mathematics is much more highly valued than quick calculation. Research also shows that if students understand a concept, they are more likely to remember the appropriate calculation and apply that calculation to a complex problem situation.
Dr. Moschkovich described additional markers of challenging mathematics, for example, that problem solving involves both concepts and procedures. Further, despite what may seem intuitive, knowing definitions is not evidence of conceptual understanding. Conceptual understanding involves making connections, including connections between familiar experiences and formal symbols, connections among mathematical representations, connections between cases and generalities, and many other types of connections. Conceptual understanding also involves using or showing the meaning of a calculation, for example, using an area model to show the meaning of multiplying two fractions. Students can also show their understanding by explaining how they arrived at a solution and justifying their thinking using multiple modes (speaking, drawing, gesturing, graphing, using symbols, etc.) to communicate mathematical ideas.
Dr. Moschovich noted that explaining and justifying mathematics often occurs in full class discussions, and often only teachers do most of the explaining and justifying. She argued that this falls short of meeting the needs of English language learners on two counts. First, English learners—or other students who may be quiet during whole class discussions—may do their best initial work individually or in small groups, and may not fully show what they know and can do in larger, more public discussions. Second, it is important for teachers to challenge students to do conceptual work. She explained that mathematics educators use “cognitive demand” of a task or lesson to rate whether students receive opportunities to give only short answers (low cognitive demand) or also are expected to express their reasoning, explain their work, and justify their answers (high cognitive demand). Supporting learners to do mathematical work that is cognitively demanding requires a task and lesson that maintains a focus on student thinking. A mix of individual work, small group informal talk, and full classroom discussions can enable all students to be able to record, revise, and express their thinking.
Dr. Moschovich also observed that many teachers focus mostly on vocabulary when working with English learners. In a sample lesson that she shared, students engaged with vocabulary to define a rectangle using the idea of “parallel” lines. As the lesson unfolded on video, it was clear that the teacher’s focus was not only on students actively using vocabulary, but also on how English learners reasoned about what “parallel” means (or the concept of “parallel”). For example, when a student described parallel lines as “they never get together,” the teacher built on that student’s thinking and supported the idea that parallel lines never meet.
Building on this example lesson, Dr. Moschovich argued that a more effective focus for pedagogy is on mathematical practices. She suggested focusing on four math practices with English learners:
In the video example, students explained parallel lines not only with words (both everyday and formal), but also with gestures. They showed they understood that lines are not limited to drawn segments, but continue into space beyond the portion that is visible. Students were clearly engaged in making sense of “parallel,” reasoning abstractly about lines, arguing for their definition of a rectangle, and describing the key properties of a rectangle.
Summarizing her key points, Dr. Moschkovich argued that the missing link in many EL classrooms is mathematical practices. In some classrooms, teachers may separate a focus on math and support for language development. In more effective classrooms, teachers address both math and language by emphasizing mathematical practices. When teachers engage students in mathematical practices like reasoning and communicating, students can develop conceptual understanding, which leads to academic success in math. By asking students to use multiple modes and multiple representations, students can also develop their language. By paying attention to language and math simultaneously, teachers can improve student participation in discussions with “math language routines.”
This means focusing on student strengths, not deficits; focusing on math practices, not vocabulary; and treating everyday/home languages as resources, not obstacles. Dr. Moschkovich explained that while these practices are important for all learners, they are essential for English learners.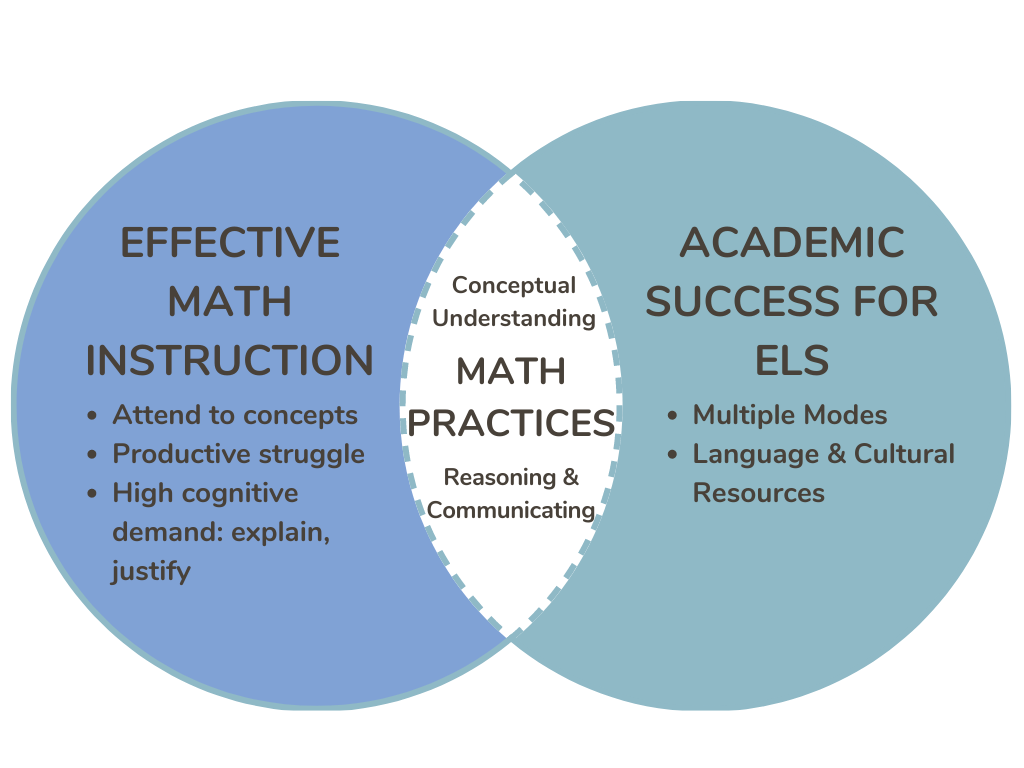
Caption: The intersection between effective math instruction and effective instruction for English learners. Created by: Dr. Judit Moschkovich; altered by: Stefani Pautz Stephenson
Alt text: A venn diagram. In the left circle, Effective Math Instruction. Attend to concepts, productive struggle, and high cognitive demand. Explain, justify. In the right circle, Academic success for ELs. Multiple Modes and language and cultural resources. In the intersection of the two circles, math practices. Conceptual understanding, reasoning and communicating.
In the breakout rooms, participants shared challenges teachers are facing, including the difficulty of teaching in English when students may speak more than one home language, finding curriculum materials for newcomers, and scaffolding student participation in oral discussions. They agreed that an effective mathematics instruction technique for English learners is providing opportunities for students to work alone, in pairs, and in small groups. An instructional cycle might include independent work, where students write what they are thinking; then pair-work, where they try out what they want to say and revise; then small group work.
The breakout rooms considered what good communication looks like in a mathematics classroom. As a starting point, they want to see discussions defined not only as teacher-led, but also as discussions where students talk more than teachers, sometimes supported by the teacher through using “math language routines.” They also stressed that communication is not only verbal: writing, drawing, gesturing, and enacting mathematics is equally important.
“I want to make sure you don’t think participation is only talk. There is such a thing as silent participation. Students who are observing intently, and moving their eyes or sitting up to look at a graph , are actually listening. Silent participation matters. You are not going to get everybody talking, even with adults. We’re not going to get everybody talking. So let’s not expect that with children,” Dr. Moschkovich stressed.
This webinar was an extension of Digital Promise’s work sponsored by the Wallace Foundation on principal leadership in a virtual environment (2021). This webinar was the second in a series, with the goals of continuing the conversation and further advancing school leaders’ understanding of current, critical topics and their application in their learning environments.
Next, on Oct. 13, 2022 at 12 p.m. ET, we’ll host “Building Systems that Support Connected Learning” with Dr. Mimi Ito. Sign up for that webinar and the full series on Eventbrite.
Want to know more about supporting English learners in the mathematics classroom? Below are resources recommended by Dr. Judit Moschkovich, as well as resources from Digital Promise:
Follow @DigitalPromise on Twitter to stay updated on upcoming research-to-practice webinars and events.
