
The Instructional Coaching for Tech-Enhanced Approaches in Mathematics (iCoachTEAM) program was designed to support instructional coaches who work with middle school mathematics teachers in using technology for HQMI. We define HQMI as instruction that emphasizes students’ development of conceptual understanding and teachers’ use of formative assessment. Conceptual understanding promotes students’ understanding of the “why” underlying steps and answers, and teachers conduct formative assessment by eliciting and responding to student reasoning.
As part of iCoachTEAM, we worked closely with instructional coaches to understand the needs of coaches and teachers to better implement HQMI. Through our continuous improvement research, we learned that identifying HQMI strategies was a challenge for coaches who were implementing subject-agnostic coaching programs. In response, we developed a collection of research-based strategies for HQMI that provided an overview of each strategy and tips on how to implement it in classrooms. The strategies were informed by a large body of research in mathematics education, which we synthesized and summarized for coaches and teachers.
One example from our research-based math instructional strategies is the Concrete – Representational – Abstract (CRA) approach. CRA is a lesson sequence for learning mathematics that begins with opportunities for students to work with concrete tools (e.g., physical or virtual manipulatives, digital simulations). After students understand the concrete representation, they connect the math concept from the concrete manipulatives to pictorial/figural representations, then connect the math concepts in the pictorial representation to abstract symbolism.
To illustrate CRA, consider the multiplication problem 23 * 5. In the concrete stage, base ten blocks can be used to build a rectangle with side lengths of 23 and 5 and show that the total area of the rectangle is 115 blocks. Students can create their own models with virtual base ten blocks. The concrete virtual manipulatives pictured below were created in Amplify Polypad, but there are many options for virtual manipulatives available online.
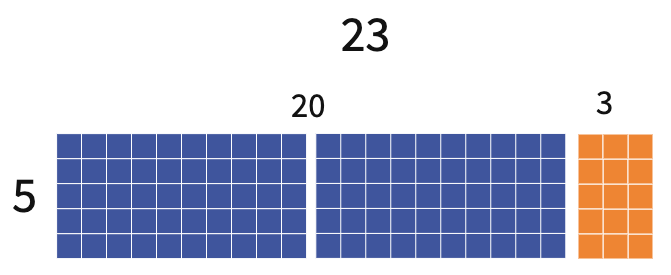
In the concrete stage, base ten blocks can be used to model 23 * 5 by building a rectangle with side lengths 23 and 5 and an area of 115 blocks.
When students are flexible and versed with the concrete modeling, they can start to connect their concrete models to a picture, such as the area model below showing the example multiplication problem. Students at this point are working with slightly more abstract representations and should be encouraged to connect their pictorial model to their original concrete model.
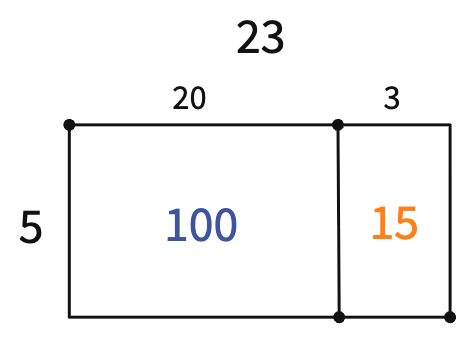
In the representational stage, students create pictures or drawings and connect them to their concrete models.
Eventually students gain comfort and fluency working with pictorial representations of mathematics concepts and are ready to connect the pictures to abstract symbols. They no longer need the concrete or pictorial representations to understand the meaning beneath the symbols, such as the expression below showing how to find the product of 23 * 5 using partial products.
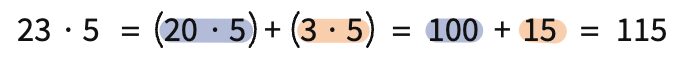
In the abstract stage, students work with abstract symbols. They have a deeper understanding of the meaning of the symbols because they were able to make connections to the mathematics concepts throughout the concrete, representational, and abstract stages.
CRA goes deeper than having students work with different representations. It prioritizes building connections between representations as a way to develop mathematical meaning. In our example, we emphasized connections students should be discussing using colors. Blue and orange are used as talking points to help students connect how the different representations convey the same mathematical meaning. The blue base ten blocks have a total area of 100 square units, the blue “100” in the area model shows the same area, and the blue highlights show where these same values are represented in the abstract symbols. Similarly, orange base ten blocks show an area of 15 square units, which connects to the orange 15 in the pictorial representation and the product 3 * 5 in the abstract symbols.

Instruction should support students in building connections between the Concrete, Representational, and Abstract stages. The red arrows emphasize the importance of these connections as students work from concrete tools to pictures and eventually to symbols.
The Concrete – Representational – Abstract instructional strategy goes deeper than having students work with different representations. It prioritizes building connections between representations as a way to develop mathematical meaning.
Technology offers tools to support CRA with virtual manipulatives and simulations that are especially useful in the concrete and representational stages. They offer a way to experiment with mathematical concepts, especially when the tool is dynamic, and allow students to move pieces, change parameters, and try out “what ifs.”